2019-03-08

行列式が面(体)積を表すことの証明的な

線形代数

二次元の平面内 $ O(0,0), \ A(a_1, a_2),\ B(b_1, b_2) $ の三点が作る三角形の面積が $ \displaystyle \frac{1}{2} |a_1b_2 - a_2b_1| $ で与えられることは、高校の数学の教科書にも乗ってる有名事実です。図形的な解釈は、鯵坂もっちょさんのこのツイートがわかりやすいです :

2×2の行列式（黒部分の面積）なら図形的に納得することができるよの図 pic.twitter.com/QHgM7N5p0s
— 鯵坂もっちょ🐟（数学のファン） (@motcho_tw) 2018年4月8日

さて、この式ですが、二つのベクトル

$\boldsymbol{a} = \overrightarrow{OA} = \left( \begin{array}{c} a_1 \\ a_2 \\ \end{array} \right) , \\
\boldsymbol{b} = \overrightarrow{OB} = \left( \begin{array}{c} b_1 \\ b_2 \\ \end{array} \right) $

を並べて作った行列 $ (\boldsymbol{a}, \boldsymbol{b}) = \left( \begin{array}{c} a_1 \ b_1 \\ a_2 \ b_2 \\ \end{array} \right) $

の行列式に見えます。これは偶然ではなく、ちゃんと理由があります。そこで、以下ではこれを示していきます。

まず、絶対値が鬱陶しいので、「符号付き面積」を定義しましょう。

平面上のベクトル $\vec{a}, \vec{b}$ のなす平行四辺形( 三角形ではない )の符号付き面積を表す関数 $S(\vec{a}, \vec{b})$ を、

原点 $ O $ に立ってベクトル $\vec{a}$ の方向を向いたときに $\vec{b}$ が左側に見えるときに正、右側にあるときに負とするように決めます( 同じ方向なら 0 )。

例えば、$\vec{e_1} = (1, 0), \ \vec{e_2} = (0, 1)$ をそれぞれx軸、y軸正方向の単位ベクトルとするとき、

$(\mathrm{i}) \ \ \ S(\vec{e_1}, \vec{e_2}) = 1$

となります。また、符号の定義の仕方からすぐ分かるように、

$(\mathrm{ii}) \ \ S(\vec{b}, \vec{a}) = -S(\vec{a}, \vec{b})$

が成り立ちます。最後に

$(\mathrm{iii}) \ S(\vec{a} + \vec{a'}, \vec{b}) = S(\vec{a}, \vec{b}) + S(\vec{a'}, \vec{b}), \\
S(\vec{a}, \vec{b} + \vec{b'}) = S(\vec{a}, \vec{b}) + S(\vec{a}, \vec{b'}), \\
S(k\vec{a}, \vec{b}) = S(\vec{a}, k\vec{b}) = kS(\vec{a}, \vec{b})$

が成り立つことに注意します。これは、下の雑な画像を見れば分かると思われます。まず第一式ですが、他方のベクトルからみた平行四辺形の「高さ」について、ベクトルの和を取ると「高さ」もその和になることが分かるでしょう。そして、第二式も三角形の相似を使えば、「高さ」も同じ倍されることが分かります。

f:id:marx_saul:20190308000354p:plain
(i) (ii) (iii) を使って、 $a = \left( \begin{array}{c} a_1 \\ a_2 \\ \end{array} \right) , \\
b = \left( \begin{array}{c} b_1 \\ b_2 \\ \end{array} \right) $ に対して

$ S(a, b) = a_1b_2 - a_2b_1 $

が成立することを示していきます。

$
\vec{a} = a_1\vec{e_1} + a_2\vec{e_2}, \ \ \vec{b} = b_1\vec{e_1} + b_2\vec{e_2}$ として
$
\begin{align}
S(\vec{a}, \vec{b}) & = S(a_1\vec{e_1} + a_2\vec{e_2}, \ \ \vec{b}) \\
& = a_1S(\vec{e_1}, \vec{b}) + a_2 S(\vec{e_2}, \vec{b}) \\
& = a_1 S(\vec{e_1}, \ \ b_1\vec{e_1} + b_2\vec{e_2}) + a_2 S(\vec{e_2}, \ \ b_1\vec{e_1} + b_2\vec{e_2}) \\
& = a_1 (\ S(\vec{e_1}, b_1\vec{e_1}) + S(\vec{e_1}, b_2\vec{e_2})\ ) + a_2 (\ S(\vec{e_2}, b_1\vec{e_1}) + S(\vec{e_2}, b_2\vec{e_2}) \ ) \\
& = a_1 (\ b_1 S(\vec{e_1}, \vec{e_1}) + b_2 S(\vec{e_1}, \vec{e_2})\ ) + a_2 (\ b_1S(\vec{e_2}, \vec{e_1}) + b_2S(\vec{e_2}, \vec{e_2}) \ ) \\
& = a_1 ( b_1 \cdot 0 + b_2 \cdot 1 ) + a_2 ( b_1 \cdot (-1) + b_2 \cdot 0 ) \\
& = a_1b_2 - a_2b_1
\end{align}
$

となって、証明されました。

さて、このクソめんどくさい、長ったらしい証明をすることによって、何か嬉しいことはあるでしょうか？今は二次元でやっただけですが、この議論の良いところは、高次元でも成り立つことです。具体的にはこう :

写像 $ f(x_1, x_2, ..., x_n ) $ が、n 個の n 次元実ベクトルに対して、実数値を返す関数であり、かつ以下の二つの条件 n重線形性、及び交代性 :

$ F(x_1, ..., x_{i-1}, kx_i + ly, x_{i+1}, ..., x_n ) \\ = kF(x_1, ..., x_{i-1}, x_i, x_{i+1}, ..., x_n ) \\ + lF(x_1, ..., x_{i-1}, y, x_{i+1}, ..., x_n ) $
$ F(x_{\sigma(1)}, x_{\sigma(2)}, ..., x_{\sigma(n)} ) \\ = \operatorname{sgn} \sigma \ F(x_1, x_2, ..., x_n ) $
( ただし、$ \sigma $ は n 次の置換で、$ \operatorname{sgn} $ は置換の符号を表す )

が成り立つとする。このとき、n 次元実ベクトル空間 $ \mathbb{R}^n $ の自然な正規直交基底 $ e_1, e_2, ..., e_n $ と、$ x_1, x_2, ..., x_n \in \mathbb{R}^n $ を順番に並べて得られる n 次正方行列 $ X $ に対し、

$ F(x_1, x_2, ..., x_n) = \operatorname{det} X \ F(e_1, e_2, ..., e_n) $

が成立する。

二次元空間の場合、さっきのように定義した符号付き面積の関数は、2次線形性と交代性を満たしていました。
したがって、行列式が出てくることは上の定理より自然なことなのです。

そして、もっと高次元でも、符号付き体積が n 次線形性と交代性を満たすことを確かめれば、上の定理より行列式の形で書けることが分かります。

2018-07-19

ベクトル空間の基底の濃度の一意性(選択公理を仮定)

タイトルままです。この言明はよく見かける割には証明をあまり見かけないので、備忘録としてここに記しておきます。

$ V $ を体 $ k $ 上のベクトル空間として、 $ A, B \subseteqq V $ をそれぞれ一次独立な集合及び基底とします。今から、$ B $ の部分集合 $ B' $ と全単射 $ B' \to A $ があることを示していきます。ここから基底の濃度の一意性は直ちに従います。

以下の条件を満たす写像 $ \varphi : B_{\varphi} \to A $ の集合族 $ \Phi = \{ \varphi \} $ を考える :

・ $ B_{\varphi} \subseteqq B $ で、 $ \varphi $ は単射
・ $ A_{\varphi} := \varphi(B_{\varphi}) \subseteqq A, \ \ \ A'_{\varphi} = A - A_{\varphi} $ として、 $ B_{\varphi} \cup A'_{\varphi} $ は一次独立

明らかに $ \Phi $ は空ではありません。なぜなら、$ B_{\varphi} = \varnothing $ で定まる唯一の写像は $ \Phi $ の元だからです。

お察しの通り、$ \Phi $ に今から半順序を入れて、ツォルンの補題を適用します。半順序は、以下のように定めます :

$ \varphi \leqq \psi \ \ \ \overset{ \mathrm{def} }{\Leftrightarrow} \ \ \ B_{\varphi} \subseteqq B_{\psi}, \ \psi|B_{\varphi} = \varphi$

すると、ツォルンの補題が適用できることはすぐさまわかります。これによって、極大元 $ \sigma $ が存在することがわかります。

$ A_{\sigma} \subsetneqq A $ と仮定すると、$ x \in A - A_{\sigma} = A'_{\sigma} $ が存在することになります。 $ B_{\sigma} \cup (A'_{\sigma} - \{ x \}) $ の張る部分ベクトル空間を $ H $ とします。 $ B_{\sigma} \cup A'_{\sigma} $ は一次独立であるから、$ x \notin H $ です。一方で $ B $ は基底なので、$ x = a_1 x_1 + \cdots + a_n x_n, \ \ \ a_i \in k, \ x_i \in B $ と表せます。ここで $ x \notin H $ だから、 $ x_i \notin H $ となる $ x_i $ があるはずです。それを、$ y $ と置くことにしましょう。

このとき、$ \tau : B_{\sigma} \cup \{ y \} \to A $ を、 $ \tau|B_{\sigma} = \sigma, \ \ \tau(y) = x $ と定めると、 $ x \notin A_{\sigma} = \sigma(B_{\sigma}) $ より、これは単射。さらに、

$ B_{\tau} \cup A'_{\tau} = B_{\sigma} \cup \{ y \} \cup (A'_{\sigma} - \{x\}) $ は一次独立です。なぜなら、 $ y \notin H $ だからです。

以上で、$ \tau \in \Phi, \ \ \sigma < \tau $ となる元が見つかり、極大性に矛盾します。以上のことから、 $ \sigma(B_{\sigma}) = A_{\sigma} = A $ で、すなわち、この写像は全単射であることがわかりました。 $ \Box $

2017-10-17

Monsky の定理 − その3 (証明)

<前
ここではいよいよ証明に入って行きます。まず前回の議論から、2-進付値の拡張 $ |\cdot|_2 : \mathbb{R} \rightarrow \mathbb{R} $ を固定しておきます。面倒なので添字の 2 は省略します。ここからは座標平面で考えましょう。まず座標を以下のように三つに塗り分けます :

$ S_1 = \{ (x_1,y_1) \in \mathbb{R} \ | \ |x_1| < 1, |y_1| < 1 \} $
$ S_2 = \{ (x_2,y_2) \in \mathbb{R} \ | \ |x_2| \geq 1, |x_2| \geq |y_2| \} $
$ S_3 = \{ (x_3,y_3) \in \mathbb{R} \ | \ |y_3| \geq 1, |y_3| > |x_3| \} $

補題を一つ用意します。

上の塗り分けについての完全三角形の面積を $ S $ とすると $ |S|_2 > 1 $ である。

三つの頂点を $ (x_1, y_1) \in S_1, \ (x_2, y_2) \in S_2, \ (x_3, y_3) \in S_3 $ としよう。ここで三角形を $ (x_1, y_1) $ が原点になるように平行移動することによっても一般性は失われない。実際
$ 1 \leq |x_2| = |x_1 + (x_2 - x_1)| \leq |x_2 - x_1| $ であり、これより $ |y_2 - y_1| \leq \operatorname{max}(|y_2|, |y_1|) \leq |x_2| \leq |x_2 - x_1| $ も得られる。また $ 1 \leq |y_3| = |y_1 + (y_3 - y_1)| \leq |y_3 - y_1| $ でありこれより $ |x_3 - x_1| \leq |x_3| < |y_3| \leq |y_3 - y_1|. $

さて、$ \displaystyle S = \frac{1}{2} |x_2y_3 - x_3y_2| $ （通常の絶対値）で与えられる。よって $ \displaystyle |S|_2 = \left| \frac{1}{2} \right|_2 |x_2y_3 - x_3y_2|_2 = 2|x_2y_3 - x_3y_2|_2. $

ここで、$ |x_2y_3|_2 = |x_2|_2 |y_3|_2 \geq 1, \ \ |x_2|_2 |y_3|_2 > |x_3|_2|y_2|_2 = |x_3y_2|_2 $ である。一般に $ |A|_2 > |B|_2 $ のとき、$ |A - B|_2 \leq |A|_2 = |B + (A-B)|_2 \leq \operatorname{max}(|B|_2, |A-B|_2) $ であり、$ |B|_2 > |A-B|_2 $ とすると $ |A|_2 \leq |B|_2 $ が得られるが矛盾するので $ |B|_2 \leq |A - B|_2 $ である。ここで $ |A - B|_2 \leq |A|_2 \leq |A - B|_2 $ を得たので、$ |A - B|_2 = |A|_2. $

ゆえに、$ 2|x_2y_3-x_3y_2|_2 = 2|x_2y_3|_2 \geq 2 > 1 $ であり補題は示された。$ \Box $

さて、いよいよ Monsky の定理の証明です。

(Monsky, 1970) 正方形が n 個の等積な三角形に分割されるとき、n は偶数である。

正方形の頂点を $ (0,0), (0,1), (1,0), (1,1) $ として、n 個の三角形による分割が与えられているとする。このとき、正方形の周の上にある 12-辺は、$ (0,0), (1,0) $ を結ぶ辺にしか現れない。$ (0,1), (1,1) $ を結ぶ辺では $ |y|_2 = 1 $ であり 1 で塗られた点がなく $ (0,0), (0,1) $ を結ぶ辺では $ |x|_2 < |y|_2 $ ゆえ 2 で塗られた点がなく、$ (1,0), (1,1) $ を結ぶ辺では $ |x|_2 = 1 $ より 1 で塗られた点がない。
$ (0,0), (1,0) $ を結ぶ辺では $ |y|_2 = 0 $ ゆえ 3 で塗られた点はない。よってこの辺の上では 12-辺しか存在しない。ゆえに $ (0,0) $ は 1 で塗られていて、 $ (1,0) $ は 2 で塗られているから、12-辺は奇数個存在しなければならず、Sperner の補題より完全三角形は少なくとも一つあり、それの面積を $ S $ とすると前の補題から $ |S|_2 > 1 $ である。ここで、等積であることを使うと $ \displaystyle S = \frac{1}{n} $ なので $ |n|_2 < 1 $ であることが分かる。もし $ n $ が奇数なら $ |n|_2 = 1 $ であるから矛盾する。よって $ n $ は偶数でなければならない。$ \Box $

少し長かったですが、これで証明が終わりました。なんとも神秘的な証明です。今の所この Sperner の補題と 2-進付値を使う証明以外のものが知られていないということがよりダイヤモンドのような神秘的な定理にしているのでしょう。

[註] 途中で選択公理を使って付値を拡張しましたが、この証明に選択公理は必要ありません。具体的には三角形分割の座標を全て有理数体に添加したものを考えるときこの体は有理数体上で有限生成なので帰納法で付値の拡大をすることができることを証明できます。そして Monsky の定理の証明の中では付値はそれで十分です。

2017-10-17

Monsky の定理 − その2 (付値)

<前後>
ここでは付値についての準備をします。少々長くなりますがお付き合いください。

体 $ K $ と全順序アーベル群 $ ( \Gamma, < ) $ 、すなわち $ a \leq c, \ b \leq d \Rightarrow a + b \leq c + d $ となる群について、写像 $ v : K \rightarrow \Gamma \cup \{ \infty \} $ が(加法)付値であるとは、以下の条件を満たすことを言う :

1. $ v(x) = \infty \Rightarrow x = 0 $
2. $ v(xy) = v(x) + v(y) $
3. $ v(x + y) \geq \operatorname{min}(v(x), v(y)) $

有理数体 $ \mathbb{Q} $ から整数 $ \mathbb{Z} $ への付値で、整数 $ n $ に対して $ \operatorname{ord_p} (n) $ を素数 $ p $ で割り切れる回数とし、$ \displaystyle \frac{a}{b} \in \mathbb{Q} $ に対して $ \displaystyle v_p \left( \frac{a}{b} \right) = \operatorname{ord_p}(a) - \operatorname{ord_p}(b) $ と定めるとこれは付値になります。

付値に対して「付値環」というものを対応させることができます。$ v : K \rightarrow \Gamma \cup \{ \infty \} $ が付値であるとするとき、$ R = \{ x \in L \ | \ v(x) \geqq 0 \} $ とすると簡単に分かるようにこれは局所環になり、任意の元 $ x \in K $ について $ x \in R $ または $ x^{-1} \in R $ が成り立ちます。付値環は自明に整域であることが分かります。

加法付値があるのでもちろん乗法付値もあります。定義は以下の通りです。

体 $ K $ について、写像 $ | \cdot | : K \rightarrow \mathbb{R} $ が乗法付値であるとは、以下の条件を満たすことを言う :

1. $ |x| \geq 0, \ |x| = 0 \Rightarrow x = 0 $
2. $ |xy| = |x| \, |y| $
3. $ |x + y| \leq |x| + |y| $

さらに、$ |x + y| \leq \operatorname{max}(|x|, |y|) $ を満たすとき、非アルキメデス的付値と言う（この条件から 3 は導くことができる）。

非アルキメデス的乗法付値 $ |\cdot| $ に対し $ v(x) = - \log |x| $ とすると加法付値になり、逆に加法付値 $ v $ に対し $ |x| = e^{-v(x)} $ とすると非アルキメデス的乗法付値になります。先ほどの $ v_2 $ によって $ |x|_2 = 2^{-v_2(x)}$ で定義するとこれは乗法付値です。これを 2-進付値と言います。

ここからは乗法付値の拡大について考察します。一般論を展開するので退屈だと思った方は、2-進付値を、乗法付値の定義を崩すことなく $ | \cdot |_2 : \mathbb{R} \rightarrow \mathbb{R} $ に拡張することができることを認めてもらえさえすれば先に進んでも全く問題ありません。

体の拡大 $ L/K $ と非アルキメデス的乗法付値 $ | \cdot | : K \rightarrow \mathbb{R} $ を考える。一般的な場合を証明する前に、まずは $ L = K(t) $ が単純拡大である場合を考察しよう。$ t $ が代数的である場合と超越的である場合に分けて考える。

まず超越的である場合から。まず $ f(t) = a_0t^n + a_1t^{n-1} + \cdots + a_n \in K[t] $ に対して、ガウスノルム $ | f(t) | = max_i( |a_i| ) $ と定める。次に $ | f(t) / g(t) | = |f(t)| - |g(t)| $ とすればこれは well-defined である。これが実際に非アルキメデス的乗法付値であることを示そう。

$ f(t), g(t) \in K[t] $ として示せば十分である。なぜなら $ \mathbb{Z} $ から $ \mathbb{Q} $ への拡張と全く同じだからである。
$ f(t) = a_0 x^n + a_1 x^{n-1} + \cdots + a_n, \ g(t) = b_0x^m + b_1x^{m-1} + \cdots + b_m $ とおく。定義の 1 は明らか。次に 2 について、$ | f(t) | = \operatorname{max}_i( |a_i| ) = |a_k|, | g(t) | = \operatorname{max}_j( |b_j| ) = | b_l | $ として、$ f(t)g(t) $ の各係数の項はみな $ a_i b_j $ という形である。$ | a_i b_j | \leq \operatorname{|a_i|, |b_j|} \leq \operatorname{|a_k|, | b_l |} $ である。ここで $ | \cdots | : K \rightarrow \mathbb{R} $ は非アルキメデス的なので定義を使うと、$ f(t)g(t) $ の係数の絶対値はみな $ max(|a_k|, |b_j| $ 以下である。ここで定め方より $ |f(t)g(t)| \leq max(|a_k|, |b_j|) = max(|f(t)|, |g(t)|). $ 逆に、 $ k+l $ 次には $ a_k b_l $ という項があるのでその次数の絶対値を取ると再び非アルキメデス性より $ |f(t)g(t)| = |a_k||b_l| .$ 最後に非アルキメデス性についてはほぼ自明なので省略する。

次に、代数的である場合だが、これはここで紹介するにはかなり長いのでここでは省略させてもらう。

単純拡大の場合に付値の拡大が可能なことをひとまず認めて示していこう。一般の $ L/K $ について、それの中間体とその上の付値の組 $ (F, |\cdot|) $ で、付値を $ K $ に制限すると与えられた付値と一致するようなもの全体のなす集合に対して、$ (F_0, |\cdot|_0) \leq (F_1, |\cdot|_1) \overset{\mathrm{def}}{\Longleftrightarrow} F_0 \subseteq F_1, |x|_0 = |x|_1, (x \in F_0) $ で半順序を入れる。ツォルンの補題を使うことで極大元が存在することが分かる。極大元 $ (F, |\cdot|) $ が、$ F \subsetneq L $ なら $ t \in L - F $ を取ることができて先ほどの議論のように付値の拡大をすれば極大性に矛盾させることができ、よって付値の拡大が存在することがわかった。

これで、ようやく準備が整いました。次からはいよいよ証明に入って行きます。

2017-10-16

Monsky の定理 − その1 (Sperner の補題)

後>

1970 年、数学者 Monsky によって次の定理が証明されました。

正方形が n 個の等積な三角形に分割されるとき、n は偶数である。

この問題は 1965 年に Fred Richman がテスト勉強に向けて準備している時に思いつき、提起されたものです。この定理はなんの変哲もない小学生にも理解できる主張をしているのに、証明の手法が非常に面白いものであるのでここで紹介します。証明には次の二つの道具を使用します。

・Sperner の補題
・2 進付値

Sperner の補題は純粋な組み合わせ論的な補題で、2 進付値は数論的な道具です。この一見何も関係がなさそうな二つを使って Monsky は鮮やかに定理を示したのです。まさに数学の持つ神秘性が現れていると思わざるを得ません。このシリーズでは二つを準備しつつ Monsky の補題をなるべく最短で証明しようとする試みであります。

ここでは Sperner の補題を証明していきます。まずは用語から。

多角形 P との三角形分割とは、三角形の辺のみが互いに共通していて、辺上に点が来たりすることはないことを言う。P の各頂点に、色 {1, 2, 3} が塗り分けられているとする。「12-辺」とは、1 が塗られた点と 2 が塗られた点を結んでできる辺のことを言う。
また、三角形が「完全」であるとは、1, 2, 3 で塗られた点を一つずつ持っている三角形のことを言う。

さて、Sperner の補題は次のことを主張します。

多角形 P の周の上にある 12-辺の個数と、三角形分割における完全な三角形の個数は、偶奇が一致する。

(証明)

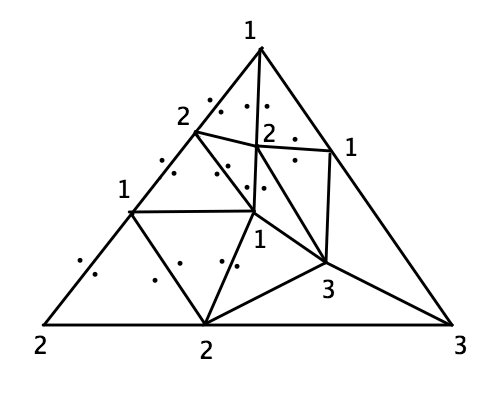
上のように、12-辺の左右に点をプロットする。多角形 P の内部にある点の個数について考える。
多角形 P の周の上にある 12-辺は多角形内部に点を 1 つ入れており、周の上にない（内部にある）12-辺は多角形内部に 2 つ点を入れている。よって、多角形 P の周の上にある 12-辺の個数と多角形の内部にある点の個数は偶奇が一致する。
次に、多角形の内部にある点の個数は、各三角形分割の内部にある点の個数の総和であるのだが、三角形が完全であるとき三角形の内部に点は奇数個あり、そうでないとき偶数個であることはすぐに分かる。したがって完全三角形の個数と、多角形の内部にある点の個数は偶奇が一致する。
以上で、 12-辺の個数と多角形の内部にある点の個数は偶奇が一致しており、完全三角形の個数と、多角形の内部にある点の個数は偶奇が一致しているから、補題は示された。$ \Box $

この Sperner の補題は非自明な結果で、次元 2 の Brower 不動点定理を導くことができます。

2017-08-19

二次の整数環の分類

群・環・体

$ n \in \mathbb{Z}$ を平方因子を持たない整数として、$ K = \mathbb{Q}(\sqrt{n}) $ の整数環（ $ \mathbb{Z} $ の整閉包）の分類をします。目標は以下を示すことです。

定理
$ K $ の整数環 $ \mathcal{O}_K $ は、

$ \mathbb{Z}[\sqrt{n}] \ \ \ \ (n \equiv 2,3 ( \operatorname{mod} 4 ) ) $
$ \displaystyle \mathbb{Z} \left[ \frac{1 + \sqrt{n}}{2} \right] \ \ \ \ (n \equiv 1 ( \operatorname{mod} 4 ) ) $

まず、上の環が $ \mathcal{O}_K $ に含まれていることは明らかです。実際、$ \sqrt{n} $ 及び $ \frac{1 + \sqrt{n}}{2} $ が $ \mathbb{Z} $ 上整であることを確かめるのは簡単です。

さて、$ \alpha \in K $ の $ \mathbb{Q} $ 上の最小多項式を $ f(x) = x^2 + ax + b $ として、$ \alpha $ が $ \mathbb{Z} $ 上整であったと仮定します。すなわち、モニックな $ g(x) \in \mathbb{Z}[x] $ があって、$ g(\alpha) = 0 $ であったとしましょう。

このとき最小多項式で割れなければいけないので、$ g(x) = f(x)h(x) $ となる $ h(x) \in \mathbb{Q}[x] $ が存在します。最高次係数に着目して、$ h(x) $ はモニックです。

ここで、適当な $ e \in \mathbb{Q} - \{ 0 \} $ があって、$ ef(x) \in \mathbb{Z}[x] $ は原始多項式になり、

$ g(x) = ( ef(x) ) ( e^{-1} h(x) ) $ となります。このとき、「一意分解整域の原始多項式が、別の多項式で商体の中で割り切れるならもとの環の中でも割り切れる」という有名なガウスの補題を使うことで $ e^{-1} h(x) \in \mathbb{Z}[x] $ となります。ところで $ h(x) $ はモニック多項式だったのですから、$ e = \pm 1 $ となります。$ ef(x) $ が原始多項式となるように $ e $ を取ったので $ f(x) $ は原始多項式、特に $ \mathbb{Z}[x] $ の元です。

以上で、$ \alpha \in K $ が $ \mathbb{Z} $ 上整ならば、最小多項式 $ f(x) $ は整数係数であることがわかりました。

$ \alpha = c + d\sqrt{n}, \ \ c, d \in \mathbb{Q} $ が $ \mathbb{Z} $ 上整、すなわち $ \alpha \in \mathcal{O}_K $ のときこれの最小多項式は

$ f(x) = (x - (c + d\sqrt{n}) ) ( x - (c - d\sqrt{n}) ) = x^2 - 2cx + (c^2 - d^2 n) $

となります。$ \alpha \in K $ が $ \mathbb{Z} $ 上整ならば、$ f(x) $ は整数係数ゆえ、$ \displaystyle c = \frac{k}{2}, \ k \in \mathbb{Z} $ とおけて、$ \displaystyle d = \frac{r}{s}, \ r,s \in \mathbb{Z}, \ s \geq 0 $ は互いに素とします。

$ \displaystyle c^2 - d^2 n = \frac{k^2s^2 - 4r^2n}{4s^2} $ が整数であることから、$ k^2s^2 - 4r^2n $ は、$ 4, s^2 $ で割り切れるので、$ 4r^2n $ は $ s^2 $ で割り切れ、$ k^2 s^2 $ は $ 4 $ で割り切れます。$ r, s $ は互いに素としたので、 $ 4n $ は $ s^2 $ で割り切れます。

$ n $ は平方因子を持たないので、$ 4n $ が $ s^2 $ で割り切れるのは、$ s = \pm 1, \pm 2 $ のときしかありえません。$ s \geq 0 $ としているので、$ s = 1, 2 $ として良いことが分かります。

以上で、$ c + d\sqrt{n} \in \mathcal{O}_K $ は $ \displaystyle c = \frac{k}{2}, \ d = \frac{r}{2}, r \ \ \ k, r \in \mathbb{Z} $ となることがわかり、ひとまず $ \displaystyle \mathcal{O}_K \subseteq \mathbb{Z} \left[ \frac{1 + \sqrt{n}}{2} \right] $ を得ます。$ n \equiv 1 $ のときは逆の包含が成り立つことは示したので $ n \equiv 1 $ のとき定理は成り立ちます。

・$ s = 2 $ のとき、$ r, s $ は互いに素としたので $ r $ は奇数です。

$ \displaystyle c^2 - d^2 n = \frac{k^2s^2 - 4r^2n}{4s^2} = \frac{k^2 - r^2 n}{4} $ は整数ゆえ $ k^2 - r^2 n $ は $ 4 $ で割り切れます。$ \operatorname{mod} 4 $ で考えると、$ k^2 - r^2 n \equiv k^2 - n \equiv 0 $ より $ k^2 \equiv n $ となります。したがって、平方因子を持たないことと、4 を法とするときの平方について考えれば $ n \equiv 1 $ となります。また、$ k $ は奇数です。

したがって、対偶を考えて $ n \equiv 2, 3 $ であれば、$ s = 1 $ であり $ d \in \mathbb{Z} $ となります。$ \displaystyle c^2 - d^2 n = \frac{k^2s^2 - 4r^2n}{4s^2} = \frac{k^2}{4} - r^2n $ は整数なので、$ k $ は偶数となって $ \displaystyle c = \frac{k}{2} \in \mathbb{Z} $ を得ます。

以上で、$ n \equiv 2, 3 $ であれば、$ c + d\sqrt{n} \in \mathcal{O}_K $ は必ず $ c, d \in \mathbb{Z} $ より、$ \mathcal{O}_K \subseteq \mathbb{Z}[\sqrt{n}] $ となります。逆の包含関係は示したので、 $ n \equiv 2, 3 $ のときも定理は成り立ちます。$ \Box $

2017-08-07

多項式の最小分解体のガロア群

群・環・体

次数の低い多項式の最小分解体のガロア群は比較的簡単に決定できます。ここでは判別式を使う方法を紹介します。

まず、K を標数が 2 でない体とする(標数 2 では使えない)。K の代数閉包 Ω を一つ用意しておく。

K 係数の n 次の既約なモニック多項式 $ f(x) = x^n + a_1 x^{n-1} \cdots + a_n $ について、K 上分離的であるとし、Ω の中での解を $ \alpha_1, \cdots, \alpha_n $ とおく(モニック性は本質的ではない)。$ L = K(\alpha_1, \cdots, \alpha_n) $ を最小分解体とする。このとき、差積と判別式をそれぞれ

$$
\Delta(f) = \prod_{i < j} (\alpha_i - \alpha_j), \\
D(f) = \Delta(f)^2
$$

と定義する。

さて、ガロア群 $ \operatorname{Gal}(L/K) $ の元 $ \sigma $ は $ \sigma(\alpha_i) = \alpha_j $ で決まり、n 次の置換とみなせるので、対称群 $ \mathfrak{S}_n $ の部分群と自然にみなせる。こうしたとき、明らかに

$$ \sigma(\Delta) = \operatorname{sgn}(\sigma) \Delta $$

が成り立つ( f は省略した)。ただし sgn は置換の符号である。

ここで、n 次の交代群を $ A_n $ と書くと、ch K ≠ 2 と f(x) が既約かつ分離的であることから差積が 0 でないことに注意して

$ \sigma \in A_n \Leftrightarrow \sigma(\Delta) = \Delta $

となる。したがって

$ \operatorname{Gal}(L/K) \subseteqq A_n $

$ \Leftrightarrow \Delta \in L $ は $ \operatorname{Gal}(L/K) $ で不変

$ \Leftrightarrow \Delta \in K $

$ \Leftrightarrow D = \Delta^2 \in K^2. $

以上で次の定理を得た :

定理
標数 2 でない体 K と K 上の既約で分離的な多項式 f(x) について、K 上の最小分解体を L とおく。
$ \operatorname{Gal}(L/K) \subseteqq A_n \Leftrightarrow D \in K^2 $

これの簡単な応用として、$ \mathbb{Q} $ 上の既約な3次多項式 $ f(x) = x^3 + ax + b, \ \ a > 0 $ の最小分解体 L のガロア群が $ \mathfrak{S}_n $ であることを示せます。
D は終結式による表現もあり、終結式を R(f, g) で書くことにすると、

$$ \displaystyle D = (-1)^{ \frac{1}{2} n (n-1) } R(f,f') $$

が成り立ちます。頑張って終結式を計算すると、$ 4a^3 + 27b^2 $ となります。$ a > 0 $ としているので、判別式 $ D $ は $ n = 3 $ より負になります。これは $ D \not\in \mathbb{Q}^2 $ を意味しており、したがって定理から $ \operatorname{Gal}(L/\mathbb{Q}) $ は交代群の部分群ではありません。

一方、与えられた多項式は3次で既約なので $ |\operatorname{Gal}(L/K)| = [L : K] \geqq 3 $ でなければならず、また、3次対称群の部分群なので $ \operatorname{Gal}(L/K) = \mathfrak{S}_3, A_3 $ であり、結局今の議論で、

$ \operatorname{Gal}(L/\mathbb{Q}) = \mathfrak{S}_3 $

がわかります。