Monsky の定理 − その1 (Sperner の補題)

後>

1970 年、数学者 Monsky によって次の定理が証明されました。

正方形が n 個の等積な三角形に分割されるとき、n は偶数である。

この問題は 1965 年に Fred Richman がテスト勉強に向けて準備している時に思いつき、提起されたものです。この定理はなんの変哲もない小学生にも理解できる主張をしているのに、証明の手法が非常に面白いものであるのでここで紹介します。証明には次の二つの道具を使用します。

・Sperner の補題
・2 進付値

Sperner の補題は純粋な組み合わせ論的な補題で、2 進付値は数論的な道具です。この一見何も関係がなさそうな二つを使って Monsky は鮮やかに定理を示したのです。まさに数学の持つ神秘性が現れていると思わざるを得ません。このシリーズでは二つを準備しつつ Monsky の補題をなるべく最短で証明しようとする試みであります。

ここでは Sperner の補題を証明していきます。まずは用語から。

多角形 P との三角形分割とは、三角形の辺のみが互いに共通していて、辺上に点が来たりすることはないことを言う。P の各頂点に、色 {1, 2, 3} が塗り分けられているとする。「12-辺」とは、1 が塗られた点と 2 が塗られた点を結んでできる辺のことを言う。
また、三角形が「完全」であるとは、1, 2, 3 で塗られた点を一つずつ持っている三角形のことを言う。

さて、Sperner の補題は次のことを主張します。

多角形 P の周の上にある 12-辺の個数と、三角形分割における完全な三角形の個数は、偶奇が一致する。

(証明)

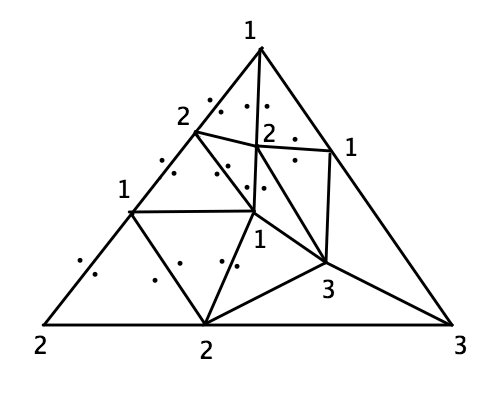
上のように、12-辺の左右に点をプロットする。多角形 P の内部にある点の個数について考える。
多角形 P の周の上にある 12-辺は多角形内部に点を 1 つ入れており、周の上にない（内部にある）12-辺 は多角形内部に 2 つ点を入れている。よって、多角形 P の周の上にある 12-辺 の個数と多角形の内部にある点の個数は偶奇が一致する。
次に、多角形の内部にある点の個数は、各三角形分割の内部にある点の個数の総和であるのだが、三角形が完全であるとき三角形の内部に点は奇数個あり、そうでないとき偶数個であることはすぐに分かる。したがって完全三角形の個数と、多角形の内部にある点の個数は偶奇が一致する。
以上で、 12-辺 の個数と多角形の内部にある点の個数は偶奇が一致しており、完全三角形の個数と、多角形の内部にある点の個数は偶奇が一致しているから、補題は示された。\( \Box \)

この Sperner の補題は非自明な結果で、次元 2 の Brower 不動点定理を導くことができます。